ZW-Formel Excel: Ideal geeignet als ETF-Sparplanrechner
Mit der ZW-Formel von Excel lässt sich spielend leicht ein sehr flexibler Sparplanrechner umsetzen, der sogar den Zinseszinseffekt mit berücksichtigt.
Es müssen lediglich ein paar Annahmen wie, erwartete Rendite, Inflation, Anlagehorizont und Sparrate getroffen werden.
Bitte auch die Kommentare ganz unten durchlesen, da diese hilfreiche Anpassungsbeschreibungen und Hinweise enthalten.
Wie ist die ZW-Formel aufgebaut?
Der Aufbau der ZW-Formel ist relativ einfach. Für die Nutzung als Sparplanrechner, habe ich einige Anpassungen vorgenommen. Diese Anpassungen ermöglichen die Eingabe der Informationen im gewohnten Format (Rendite in % pro Jahr,…).
Aufbau

Eingabegrößen
[Rendite, %/Jahr] /12
Die erwartete (nicht garantierte 🙂 ) Rendite in % pro Jahr. Diese wird durch 12 dividiert, da die ZW-Formel eine Eingabe in Monaten haben möchte. Hier kann auch die Inflation berücksichtigt werden, indem ich die Formel wie folgt anpasse: ([Rendite %/Jahr] – [Inflation %/Jahr]) /12
[Anlagehorizont, Jahre] *12
Der Anlagehorizont in Jahren. Dieser wird mit 12 multipliziert, da die ZW-Formel eine Eingabe in Monaten haben möchte.
-1* [Sparrate, €/Monat]
Die monatliche Sparrate in € pro Monat. Diese wird mit -1 multipliziert, da die ZW-Formel das so haben möchte, um ein korrektes Ergebnis zu liefern.
ETF-Sparplanrechner Schritt-für-Schritt
Die Nutzung der ZW-Formel für einen Sparplanrechner wird nachfolgend, Schritt-für-Schritt, anhand eines konkreten Beispiels umgesetzt.
Beispiel 50€ Sparplan
Angenommen, ich möchte für mein Kind einen Sparplan über 18 Jahre zu monatlich 50€ einrichten und wissen, mit welchem Endwert ich circa rechnen kann. Dabei soll der Zinseszins, die von mir erwartete Rendite und die erwartete Inflation auch berücksichtigt werden.
- Leeres Excel Blatt öffnen
- Eingabe der monatlichen Sparrate [€] in B1, hier 50€
- Eingabe der erwarteten jährlichen Rendite [%] in B2, hier 5%
- Eingabe der erwarteten jährlichen Inflation [%] in B3, hier 2%
- Eingabe des Anlagehorizonts [Jahre] in B4, hier 18 Jahre
- Eingabe der ZW-Formel in B5:


Wichtig ist die korrekte Formatierung der Eingabezellen, speziell bei der Eingabe von Rendite und Inflation in %.
Wenn man Rendite und Inflation jeweils mit 0% befüllt, liefert die Formel einen Endwert, der dem eingezahlten Sparbetrag entspricht. Bei meinen Berechnungen gehe ich stets konservativ vor und rechne mit 5% erwarteter Rendite, bei 2% erwarteter Inflation.

Danke für den Artikel,
das ist eine schöne Rechenspielerei, die einen auch motiviert, eine höhere Sparrate zu erreichen um die Zahl unten entsprechend höher werden zu lassen.
Auch ich träume bei dem Zahlenspiel gerne von den höheren Renditen weil das Ergebis toll ablesen lässt. Das Leben und die Wirtschaft bzw auch der eigene Job schreibt aber meist seine eigenen Geschichten sodass man wirklich auch konservativ rechnen sollte um nicht enttäuscht zu werden.
Interessant auch zu sehen wie das eigene Geld an Wert verliert wenn man es nur auf dem Konto liegen lassen würde (Inflation eingetragen aber kein Zins)…
Hallo Nils,
danke für deinen Kommentar und den Hinweis mit der Inflation. Es freut mich, wenn der Beitrag hilfreich ist. Man bekommt mit der Formel spielerisch ein gutes Gefühl für den Zinseszinseffekt und die Inflation. Auch immer wieder überraschend finde ich die hohen Beträge, die nach einem Anlagehorizont von mehr als 10 Jahren, bei relativ kleinen monatlichen Sparraten zustande kommen.
Viele Grüße
Martin (Finanz-Ingenieur)
Gutes und vor allem realistisches Rechenbeispiel, dass auch ein Laie nach kurzem Überlegen verstehen sollte 🙂 Ein 50€-Sparplan ist aus meiner Sicht immer der beste Einstieg, da das jeder hinbekommen sollte.
Hallo vielen Dank für die gute Erläuterung.
ETF’s haben zusätzlich noch Die Verwaltungsgebühr, die anteilig und monatlich von der Wertentwicklung abgezogen und direkt aus dem Fondsvermögen entnommen wird.
Wie würde das denn in Excel aussehen?
Hallo Tobias,
es freut mich, wenn der Beitrag hilfreich ist.
Das ist korrekt, man spricht auch vom Total Expense Ratio (TER) des jeweiligen ETFs.
Umsetzung in Excel könnte so aussehen:
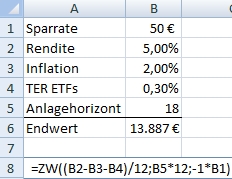
Viele Grüße, Martin
Hallo, danke für die Formel. Wie müsste ich die Formel ändern, wenn zu Anfang schon einen kleinen Betrag investieren möchte und auf diesem durch die Sparrate aufbauen möchte? Sprich, ich möchte beispielsweise zu Anfang 2000€ investieren und ab diesem Zeitpunkt eine Sparrate von 50€ nutzen?
Vielen Dank!
Hallo Sebastian,
das könnte dann so aussehen:
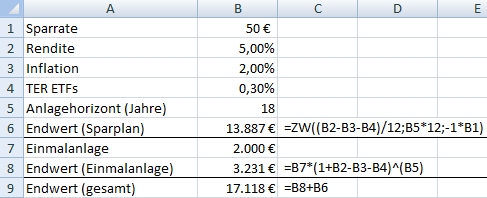
Die Berechnung für die Einmalanlage erfolgt separat und wird mit dem Endwert der Sparrate addiert.
Viele Grüße, Martin
Vielen Dank Martin, darauf hätte ich auch kommen können. 🙂
Gerne, so können es andere auch nachlesen 🙂
Hallo,
vielen Dank für die Formel.
was muss ich bei dieser formel hinzufügen um zum Beispiel eine Dynamik von 5% bei einem Banksparplan mit einzubeziehen
also im 1. jahr 100€
im 2. jahr dann 105€
und im 3. dann 110,25€
Damit ich es nicht einzeln ausrechnen muss, sondern die Formel das erledigt
Vielen Dank für diese Formel.
Hallo,
das hilft mir wirklich weiter! Vielen lieben Dank das du das öffentlich und kostenlos weitergibst :).
was ist denn wenn ich 8 Sparpläne laufen habe – sprich eine Asset Allocation? Ich hätte jetzt für jedes einzelne Asset das gerechnet, aber das stimmt dann nicht so ganz, oder?
Hallo Patricia,
es freut mich, wenn der Inhalt hier hilfreich ist.
Grundsätzlich muss man sagen, dass diese Formel nur ein sehr grobes „Schätzeisen“ ist. Das Ergebnis hängt maßgeblich von diversen Annahmen ab:
Nachfolgende Renditeangaben beziehen sich auf das interaktive Kalkulations-Tool von growney*
Damit soll man ein Gefühl dafür bekommen, welche Renditen bei einem weltweit diversifizierten ETF-Portfolio (hier 100% Aktien), für einen Sparplan und für eine Einmalanlage jeweils bei einer schwachen Wertentwicklung möglich sein könnten. Dabei beschränken wir uns bewusst nur auf die schwache Wertentwicklung pro Jahr und vergleichen diese mit eine der langfristig zu erwartenden, durchschnittlichen Wertentwicklung pro Jahr, aufgetragen über einen Anlagehorizont von 30 Jahren. Diese Betrachtung soll ein Gefühl für das Risiko vermitteln.
Zu deiner Frage: Ich denke, man kann es entweder für alle 8 Sparpläne einzeln rechnen, wenn die getroffenen Annahmen bzgl. Rendite unterschiedlich sind. Andernfalls könnte man auch alles zusammenfassen. Egal wie man es macht, die getroffenen Annahmen spielen eine enorme Rolle.
Viele Grüße
Hallo,
erst einmal vielen Dank für die Formel. Sie hat mir sehr geholfen. Habe aber noch eine Frage.
Wie genau kommt man auf diese Formel bzw. wie sieht sie in mathematischer Schreibweise aus? Habe schon herumgesucht aber nichts dazu gefunden.
Grüße
Hallo Christian,
vielen Dank für deinen Kommentar.
Die mathematische Schreibweise kann ich dir spontan nicht liefern, werde mich aber damit beschäftigen und auf dem Blog ergänzen.
Damals hatte ich Gegenproben mit diversen Online-Rechnern gemacht und die Ergebnisse waren deckungsgleich.
Falls jemand die Antwort kennt, gerne hier posten.
Viele Grüße
Martin
Hallo,
danke für den Beitrag. Super!
Eine Frage habe ich noch. Es geht um den Ausgabeaufschlag. Wie rechne ich diesen mit in die Formel, der bezieht sich bei dem monatlichen Sparen ja pro Kauf. Die restlichen Eingaben beziehen sich ja auf das Jahr.
Hallo Danny,
es freut mich, wenn der Beitrag hilfreich ist. Einen Ausgabeaufschlag mit einarbeiten könnte dann so aussehen:
Editiert 27.02.2019: Zellenbezüge im nachfolgendem Bild korrigiert.
Der Ausgabeaufschlag reduziert die monatliche Sparrate in der Formel.
Frage am Rande: Wieso Ausgabeaufschlag bezahlen? Viele sparpläne bei Robo-Advisors oder auch ETF-Sparpläne bei Online-/Direkt-Banken sind kostenlos in der Ausführung.
Viele Grüße
Martin
Hallo Martin,
Vorab vielen Dank für deine tolle Hilfestellung!
Leider kann die letzte Formel für die Einmalanlage durch die Einbeziehung des Ausgabeaufschlags nun nicht mehr stimmen (=Zeilenverschiebung). Muss dieser Aufschlag dabei auch berücksichtigt werden?
Danke im Voraus,
LG Chris
Hallo Chris,
vielen Dank für den Hinweis auf den falschen (jetzt korrigierten) Zellenbezug in meinem Kommentar vom 27.01.2019
Du hast Recht. Wenn der Ausgabeaufschlag auch auf die Einmalanlage anfällt, was denke ich der Fall sein sollte, könnte die Rechnung wie folgt aussehen:
Viele Grüße
Martin